期末作业,码字码了2个小时,不发上来感觉自己亏了一个亿。以下是实践报告节选。
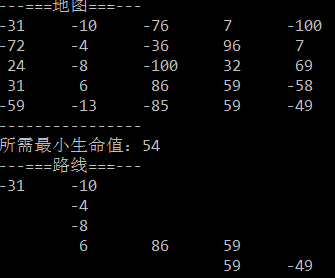
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M×N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。 骑士需要知道为能够拯救到公主所需的最低初始健康点数。
题目中提到了由许多“房间”组成的“地下城”,而每个房间都有“对骑士造成的伤害”这个数据。此外与每个房间毗邻的房间不尽相同。因此,有两个重要的数据结构需要我们设计:“房间”、“地下城”。
对于房间,我们有这些数据需要处理:进入这个房间,骑士可获得的生命值(负数则表示进入这个房间会失去生命值)、骑士进入这个房间后可以进入的下一个房间、以及算法所需要用到的两个数据(假设这个房间是起点,骑士接下来应该要走的房间,以及到达终点时,所受到的最大伤害)。

对于“地下室”,所需要储存的,自然是关于“房间”的信息:每个房间可以给予骑士的最大/最小生命值、M和N的值、储存房间数据的“房间数组”。

为了解决题目给出的问题。我们有2件事需要处理:地下城的生成、最佳路径的计算。其中最为重要的是后者。
生成的代码十分简单:先创建一个保存所有房间的数组。再生成每个房间的数据(可恢复的生命值、右方和下方的房间)。

计算的代码较为复杂,需要着重讨论。
对于一个任意的地下城,我们有多条路径可供选择,但是只有一条(也可能是多条,取其中一条)是题目所需要的答案。M和N的值越大,可选路径就越多。如果我们每一条路都走一遍,再从中挑出我们需要的答案,计算量无疑是十分巨大的。因此我们换种思路:不通过路径得到答案,而是通过房间本身得到答案。有没有一种算法,只需要每个房间仅遍历一遍,就能得到答案呢?如果有的话,计算量将会小的很多——因为对于一个M×N的房间,有
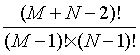
条路径可供选择,但只有M×N房间需要遍历。如果M和N均为100,那么有2.3×10^58条路径(如果地球上每个人拥有10亿台计算机、每台计算机并行处理10亿个线程,每个线程每秒处理10亿条路径,那么至少需要100万亿个世纪处理数据——宇宙的年龄都不及其十万分之一)可供选择和1.0×10^4个房间需要遍历——相差了54个数量级!
所以这个“每个房间只遍历一遍”的算法存在吗?答案是肯定的。
我们从一个小小的例子出发:一个2×2的地下城。很显然,这个地下城只有两条路可以走:先右后下、先下后右。因为起点和终点是一样的,因此答案十分明显——右边和下边的房间,哪个房间加的生命值多/扣的生命值少,就走哪间。我们不妨把结论存储下来——在这个房间,我们应该往哪个房间走、以及这么走,最多会失去多少生命值的结论。
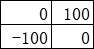
接下来我们将这个地下城“扩建”,变为更大的地下城:
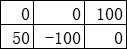
以上图为例,我们应该怎么走呢?起点下方恢复的生命值比右方的更多,显得十分诱人——但我们应该先向下走吗?其实,我们可以很轻松地计算出来,“新”起点是原起点下方的房间的话,所受到的最大伤害是50。所以,与其先走下方的房间(并在之后的房间挨揍),不如先走右边的房间,最后按照原先2×2的地下城的走法来走(这样走,骑士一开始只需要1点生命值)。
通过这种方法,不管是多大的地下城。我们都可以先处理最靠近终点房间,每个房间只需要处理一次,之后再处理离终点较远的房间。如此,我们不需要人手10亿台计算机也能解决M和N值较大的地下城问题。
既然算法有了,那么要怎么实现这个算法呢?
当我们生成所需要的地下城后,我们可以按照这个顺序处理每个房间:

沿着斜线依次处理每个房间(因为每个房间所需要的数据包含在自身以及右方和下方的房间中),这样处理的话不会出现右边/下边的房间还没有所需要的数据的情况。
这么做的缺点也十分明显——跳转太过频繁。还是上方出现的“地下城”,我们为每个房间标号:
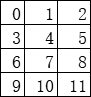
那么我们要遍历的顺序为11→10→8→9→7→2→6→4→2→3→1→0。需要额外的控制“当前处理房间”的代码。
我们可以用一个更加简单的方式遍历房间——依照序号倒着遍历,也就是从右到左,从下到上。这么做同样不会出现右侧/下侧房间没有所需数据的问题。而且遍历起来更加方便。
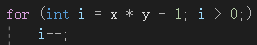
(这里i初始不是x * y(就是M × N)是因为对终点的处理放在了循环之外)
按照这个顺序,我们对每个房间进行处理。
对于终点,因为其右方和下方都没有房间。可以放在循环之外单独处理,这样循环内部不用判断每个房间是不是终点。

接下来是剩下的房间。对于每个房间,我们先判断它的右方和下方有没有房间可以走。

接下来分别读取可以走的房间的数据,并确定应该走哪个房间。

最后,把“以这个房间为起点所受到的最大伤害”存起来。
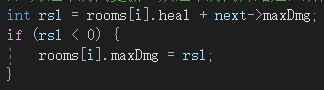
最后从起点开始,一路读取起点的next(接下来要走的房间),next的next,next的next的next……最后读取到终点为止(只有终点的next为NULL,当读取到next为NULL的房间时就可以停止了),并将结果输出即可。
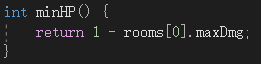
至于所需要的最小生命值——